哈希思想

思想核心

哈希思想的核心是通过哈希函数将任意输入映射为固定长度的输出（哈希值），利用这种映射的高效性、唯一性和确定性解决问题。

广泛应用

这种思想在计算机科学及相关领域被广泛借鉴和扩展，比如：

• 在数据结构中，利用哈希思想实现布隆过滤器、一致性哈希、哈希链表等。
• 在算法优化中，利用哈希思想实现快速查找和去重、字符串匹配、随机化算法等。
• 在安全应用中，利用哈希思想实现MD5校验、SHA校验、软件签名、密码加盐、区块链、数字签名与验证等
• 在分布式系统中，利用哈希思想实现数据分片与路由、P2P网络资源定位等。
• 在网络协议优化中，利用哈希思想实现哈希路由、流量分类与监控等。
• 在存储与文件系统中，利用哈希思想实现重复数据删除、哈希索引等、文件系统元数据管理等。
• 在机器学习与数据科学中，利用哈希思想实现哈希编码、局部敏感哈希等。

下面，对一些常见的应用做简易介绍：

布隆过滤器

利用多个哈希函数判断元素是否存在，空间效率极高（仅需少量比特位），虽有概率误判但适用于缓存穿透、垃圾邮件过滤等场景，如： Redis 的布隆过滤器。

一致性哈希

在分布式系统中，将节点和数据映射到环形哈希空间，解决节点动态增减时的数据迁移问题，如：分布式缓存 Memcached、Kubernetes 的服务发现。

密码加盐

加盐哈希（Salted Hash）将用户密码与随机盐值混合哈希，防止彩虹表攻击。如： Linux 的 shadow 文件、Web 应用的密码存储。

哈希链表

像 Java 中的 HashMap、HashSet，底层实现就是基于哈希思想实现的。

哈希表，一种 K-V 形式的数据结构。这种结构用途甚多，如：数据缓存、哈希索引、密码存储。数据缓存可以应对高并发访问；哈希索引是数据库索引类型之一，同样是将数据进行哈希运算后根据哈希值存储到对应的哈希桶里，哈希索引适合等值查询，在范围查询上性能不佳。而密码存储可以将明文密码进行哈希运算后存入数据库，确保敏感数据的安全性。

P2P网络资源定位（迅雷种子下载）

BitTorrent 用 SHA-1 哈希值标识文件块（Info Hash），节点通过 Kademlia 协议的哈希表（DHT）快速查找资源所在节点。

哈希函数

函数作用

使用哈希函数，我们可以：

1. 将非整数（如字符串）键映射成整数键 高效存取
2. 将大整数映射成较小的整数 合理分配空间

// 假设我们要存储的8位数电话码有1亿个，我们可以有两种选择

// 聪明的选择：使用hash表存储，只需定义一个有997个存储单元的数组，即 M[997]。
hash(v)=v%997 ;
hash(66752378)=237;
hash(68744483)=336;

// 愚笨的选择：初始化一个有1亿个存储单元的数组
M[100000000];
M[0]=66752378;
M[2]=68744483;
M[...]=...;
M[99999999]=68744488;

// 在数组空间的利用上，数组M[997]在量级上比M[100000000]缩小了1000倍以上。

最佳实践

一个好的哈希函数，应该满足以下条件：

1. 快速计算，算法复杂度为 O(1)。
2. 散列表的长度 M 尽可能的小。
3. 键值尽可能均匀分布在不同的索引列中。
4. 冲突尽可能地小。

因此，最好和最受欢迎的哈希函数的实现：

// 整数的哈希函数
hash_number(v)=v%M; // v=值，M=散列表的长度

// 字符串的哈希函数
int hash_function(string v) { // 假设 1: v 只使用 ['A'..'Z']
  int sum = 0;                // 假设 2: v 是一个短字符串
  for (auto& c : v) // 对于 v 中的每个字符 c
    sum = ((sum*26)%M + (c-'A'+1))%M; // M 是表大小
  return sum;
}

对于散列表长度M的设定，要考虑负载因子不能超过0.5，否则会出现：

• 增加哈希冲突
• 查询、插入、删除的操作性能下降
• 内存使用效率降低

因此，我们可以根据负载因子的公式，大致估算散列表长度M。

// 【公式】负载因子a = 键值数量N ÷ 散列表长度M

// 【示例】键值数量N≈11，负载因子a＜0.5，那么散列表长度M=23（在22附近找一个质数作为散列表长度）

哈希冲突

经过哈希函数运算后的值，可能存在相同情况，进而导致 K-V 出现一对多映射，从而引发冲突问题。

冲突的根本原因是通过哈希函数”将大整数映射成较小整数“时，我们的哈希函数会导致 K-V 出现一对多，即 V₁→K，V₂→K，违背了一对一原则。

哈希冲突是哈希数据结构的无法避免的核心问题，只有解决了”哈希冲突“，才能保证数据的完整性。

冲突解决

可以使用链地址法和开放寻址法解决哈希的键值冲突问题，由于 Java 的 HashMap 和 HashSet 都是基于链地址法解决键值冲突，因此作为重点内容把握。

链地址法（掌握）

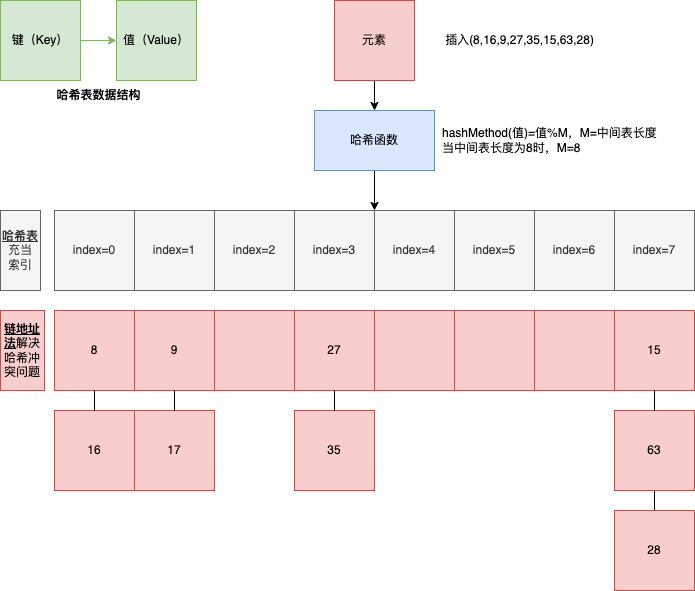
链地址法的基本原理：将所有哈希值相同的元素存储在一个链表中，哈希表的每个位置对应一个链表。当插入一个新元素时，计算其哈希值，然后将元素插入到对应的链表中。

这种方式能大幅降低哈希表的大小，因为可以通过链表来动态地扩展存储空间，适应不同数量的元素。正因如此，Java 的 HashSet 和 HashMap 都是基于此种方式解决哈希冲突问题。

20170630-哈希表思想

开放寻址法（了解）

开放寻址的基本原理：当发生冲突时，通过某种探测序列在哈希表中寻找下一个空的位置来存储新元素。

比如：线性探测法就是依次探测下一个位置，直到找到空位置；二次探测法是按照二次函数的方式来确定探测步长。

这种方式是直接将**值（Value）**存储到在哈希表中，没有通过额外的存储空间解决键值冲突问题，当哈希表未满时，总能找到位置存储新元素。

• 优点

  • 节省空间。不需要额外的链表或其他数据结构来处理冲突
  • 查询效率高。在没有出冲突或冲突很少的情况下，查询速度非常快。只需要根据哈希值直接定位到值的位置。

• 缺点

  • 容易产生聚集现象。随着元素的增加，哈希冲突会导致大量元素堆积在某些区域，进而导致查询和插入效率下降。
  • 删除操作复杂。删除元素时，不能简单地将元素所在位置置空，需要进行标记处理，否则会影响后续查找。

后记

至此，哈希思想的核心内容均已凝练在此文中。